Medellín, Abril de 2010
JÚPITER
M1 > 25 M2
M3 mucho menor que M1 y M2
M2 órbita alrededor de M1.
M3 orbita con M2 alrededor de M1
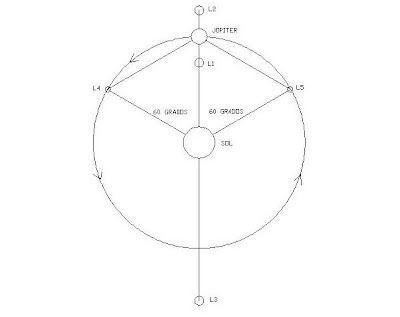
Figura 1 Sistema Sol – Júpiter - Asteroides
L4 va adelante en la órbita de tal manera que L4, Sol y Júpiter forman un triángulo equilátero. L5 va siguiendo a Júpiter e igual que en el caso anterior, Sol-Júpiter y L5 forman un triángulo equilátero.
2. 2. No hay claridad sobre la relación exacta de las masas de los tres cuerpos.
En los puntos L1, L2 y L3 la disposición de las líneas equipotenciales, forma un paraboloide hiperbólico (una silla de montar) y por tanto, cualquier acción externa al sistema, puede sacar a M3 de la configuración estable. No sucede lo mismo con los puntos L4 y L 5 (los vértices exteriores del los triángulos equiláteros) en los cuales la configuración de las equipotenciales es un paraboloide elíptico, es decir un hueco y por tanto no es fácil que M3 pueda salir de ahí.
Por lo tanto los puntos L1, L2 y L3 son inestables, mientras que L4 y L5 son estables.
Figura 2
http://en.wikipedia.org/wiki/Jupiter_Trojan
La idea de nombrar a los asteroides de Júpiter ubicados en L4 y L5 con nombres de los héroes de la Guerra de Troya fue sugerida por los astrónomos que identificaron el fenómeno. Los asteroides del grupo L5 recibieron el nombre de los héroes de Troya (campo troyano), mientras que los del L4 recibieron nombres de sus oponentes en la guerra de Troya, es decir los griegos. De todos modos, existen algunas excepciones, como 617 Patroclo, nombre griego para un asteroide del campo troyano, o 624 Héctor, nombre troyano en campo griego, que le fueron dados con anterioridad a la convención de nombres.
Los Troyanos y los griegos, además del movimiento de traslación alrededor de Júpiter, que tarda 12 años, tienen un movimiento en sentido horario alrededor de una figura que es como una lágrima, que es la que denominamos halo. Esta translación interna en cada halo, en sentido horario, tiene un periodo cercano a los 200 años.
Figura 3 Periodos de los troyanos en sus halos
Héctor es el más grande de los asteroides troyanos, y se encuentra en el grupo de los griegos, con un diámetro aproximado de 250 km (aunque de forma muy irregular).
Figura 4 Apariencia de un asteroide troyano.
La ubicación de un satélite, en cualquiera de los puntos de libración, depende del uso que se le va a dar al satélite. No obstante, si el satélite es colocado en L1, L2 o L3 cualquier fuerza exterior lo va a sacar de la estabilidad orbital. Si se ubica en L4 o L5 la estabilidad del satélite, no está garantizada totalmente, pero la probabilidad de que se mantenga estable su órbita es mucho mayor, que si se hubiera ubicado en L1, L2 o L3.



No hay comentarios:
Publicar un comentario